原文題目

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

題目摘要

1. 問題描述：給定一個 m x n 的二維矩陣，這個矩陣具有「每一列的數字從上到下遞增排序」和「每一行的數字從左到右遞增排序」特性，請找出目標數值 target 是否存在於這個矩陣中。
2. 輸入：matrix：二維矩陣（m x n）、target：需要查找的目標數值。
3. 輸出：如果目標數值存在於矩陣中，回傳 true，否則回傳 false。

Example 1:

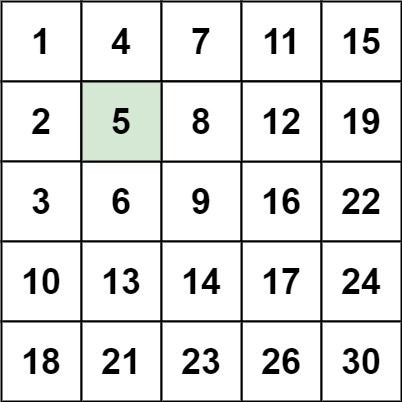
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

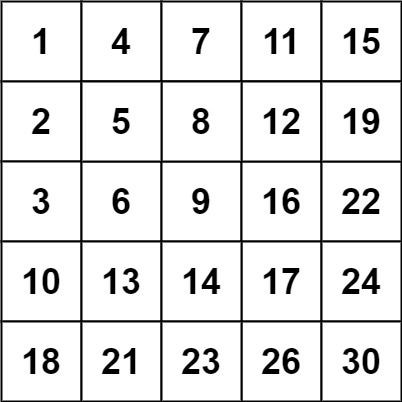
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

解題思路

1. 選擇起始點：
   • 我們從矩陣的右上角開始進行搜尋，這個位置是該行中最大的數字，同時也是該列中最小的數字。這樣的選擇能夠有效利用矩陣的排序特性。
2. 設定指針：
   • 使用兩個指針：row 初始為 0（指向第一行），col 初始為 matrix[0].length - 1（指向最後一列）。
3. 進行搜尋：
   • 如果當前元素等於目標值 (target == matrix[row][col])，直接返回 true，表示找到了目標值。
   • 如果當前元素小於目標值 (target > matrix[row][col])，因為該行的數字都是遞增的，所以可以向下移動到下一行（row++），搜尋更大的數字。
   • 如果當前元素大於目標值 (target < matrix[row][col])，由於該列的數字也是遞增的，因此可以向左移動到前一列（col--），搜尋更小的數字。
4. 結束搜尋：
   • 如果在整個搜尋過程中未找到目標值，當指針超出矩陣的範圍時，回傳 false，表示目標值不存在於矩陣中。

程式碼

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        //從右上角開始做搜尋，行指針從矩陣的第一行開始、列指針從最後一列開始
        int row = 0;
        int col = matrix[0].length-1;
        while (row<matrix.length && col>=0) { //設定邊界條件
            if (target == matrix[row][col]) { //如果當前元素等於目標值
                return true; //回傳true
            }
            else if (target>matrix[row][col]) { //如果當前元素小於目標值
                row++; //移動到下一行
            }
            else { //如果當前元素大於目標值
                col--; //移動到上一列
            }
        }
        return false; //如果沒有找到回傳false
    }

結論： 在日常生活中，假設你在一家大型書店中尋找一本特定的書。這家書店的書架上，每一行的書都是按字母順序排列，而每一列的書也是如此。這樣的排列方式使得尋找變得高效而簡單。這一題就是利用這種排列特性來快速查找目標值。透過從右上角開始搜尋，如果當前書籍的編號小於你要找的書編，就往下找；如果大於，則往左找。這樣不斷縮小範圍，最終能迅速找到書籍或確認它不存在。這種方法不僅節省了時間，也讓搜尋過程變得更加有趣與高效！